The big O notation is very essential for the evaluation of algorithms. We want to have a solid understanding of this notation and how to use this in the future. we are going to talk about the massive O notation in the course of this phase.

Our algorithm for finding the books and placing them has n number of objects. For the first book search, it’s going to evaluate n number of books for the worst case situation. If we are saying time complexity is T, then for the primary e book the time complexity may be:

T(1) = n

As we are eliminating the founded book from the listing, the scale of the list is now n-1. For the second e-book seek, it’s going to evaluate n-1 wide variety of books for the worst case scenario. Then for the second one ebook, the time complexity could be n-1. Combining the each time complexities, for first two books it’ll be:

T(2) = n + (n - 1)

If we hold like this, after the n-1 steps the ultimate book seek will most effective have 1 e-book left to evaluate. So, the overall complexity will look like:

T(n) = n + (n - 1) + (n - 2) + . . . . . . .  . . . . + 3 + 2 + 1 

Now if we take a look at the previous series, would not it appearance acquainted? it’s also known as the sum of n numbers equation as proven:

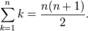
So we can write:

T(n) = n(n + 1)/2 

Or:

T(n) = n2/2 + n/2 

For asymptotic evaluation, we ignore low order phrases and steady multipliers. on account that we have n2, we will effortlessly ignore the n right here. additionally, the half of constant multiplier also can be not noted. Now we will express the time complexity with the big O notation as the order of n squared:

T(n) = O(n2) 

throughout the book, we can be using this huge O notation to explain complexity of the algorithms or operations. right here are some commonplace huge O notations: